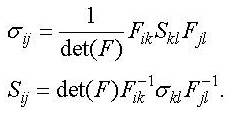Computational Modeling of Stents in Arteries

To perform mechanical analysis of stents in atherosclerotic arteries, it is obviously important to have an understanding of solid continuum mechanics.  They governing equation that applies to the stent, artery, and plaque is the conservation of linear momentum.  It is this vector equation that must be solved using the finite element method (which will be shown later).  In Cartesian coordinates, this governing equation can be expressed as

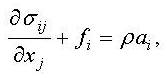
where i, j = 1,2,3.  Here, σ_ij is the Cauchy stress tensor, x_i refers to the deformed coordinates, ρ is the density of the material, f_i is the body force vector, and a_i is the acceleration vector.  The acceleration a_i can be expressed in terms of the material derivative of the velocity v_i as

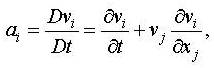
and the velocity v_i can be expressed in terms of the material derivative of the displacement u_i as

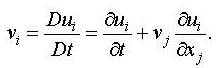
For small (infinitesimal)  displacements and velocities, it is possible to ignore the nonlinear terms in the material derivatives [6].  However, since the deformation of the stent and arterial wall can be large (much greater than 1%), the theory of nonlinear mechanics becomes necessary.  The deformation gradient tensor and the left Cauchy-Green tensor are important in the study of large deformations.  The deformation gradient tensor F_ij is defined as

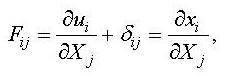
where i, j = 1,2,3, and u_i = x_i - X_i (i = 1,2,3) is the displacement vector.  X_i refers to the undeformed coordinates, and xi refers to the deformed coordinates.  Note that δ_ij is called the Kronecker-Delta and it is equal to 1 when i = j and 0 when i ≠ j.  Then the left Cauchy-Green tensor B_ij can be defined in terms of F_ij as [7]

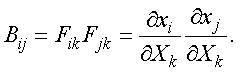
Often, it is mathematically easier to describe the displacement in terms of the strain tensor.  There are many kinds of finite strains used in nonlinear mechanics.  For instance, the Green’s strain tensor is defined as [7]

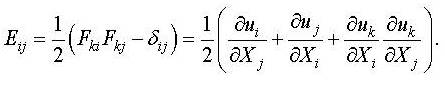
The term "finite" refers to large deformations in which nonlinear terms are present.  Furthermore, there are also many kinds of finite stresses that are useful in nonlinear mechanics as well.  The second Piola-Kirchhoff stress tensor S_ij is sometimes mathematically more convenient than the Cauchy stress tensor σ_ij.  The former is used in the mathematical description of the material properties; this can be done by using a strain energy function.  For more information on this, please see Material Properties.  The Cauchy stress tensor is used in the conservation of linear momentum equations, as shown above.  The two are related by [7]

.