Computational Modeling of Stents in Arteries

In order solve for stresses and displacements in the arterial wall, stent, and plaque, the constitutive equation of these materials must be determined.  The reason why two materials will deform in different ways even though the same load distribution is applied is due to the differences in the constitutive equations.  If these equations are known, then it is possible to solve the governing equations (conservation of linear momentum equation) subjected to specific boundary conditions using the finite element method.  The task of determining the constitutive equation can be a difficult task because of nonlinearity, non-uniformity, and anisotropy of the materials.  Generally speaking, the constitutive equation relates the stresses and the strains (which are functions of the displacement u_i).  For materials that behave in a nonlinear fashion, it is more convenient to use a strain energy function W to define the constitutive equation.  The second Piola-Kirchhoff stress tensor S_ij is related to W by

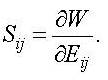
where E_ij is Green’s strain tensor [6].  It has been experimentally determined that the arterial wall is relatively incompressible [8].  As a result, many have used the general Mooney-Rivin hyperelastic constitutive equation for the arterial wall.  The nonlinear material properties of plaque have also been modeled using this equation.  The strain energy function for the generalized Mooney-Rivlin solid is [10]

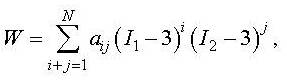
where I₁ and I₂ are the invariants of the left Cauchy-Green tensor B_ij.  If N = 1, then there are 2 material constants a₀₁ and a₁₀.  If N = 2, then there are 5 material constants a₀₁, a₁₀, a₁₁, a₀₂, and a₂₀ [11].  Of course, the material constants will differ for the plaque and the arterial wall.  The Mooney-Rivlin model assumes that the material is isotropic as well since the strain energy function is expressed in terms of the two invariants [12].  However, the arterial wall is actually anisotropic because of the orientation of the collagen fibers [8].  As a consequence, some have tried to use the energy function of the form

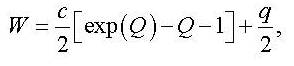
where c is a constant and Q and q are quadratic functions of the Green’s strains (E₁₁, E₁₂, E₁₃, etc.) [6].  Many other types of constitutive equations can be found in the literature regarding the arterial wall and plaque.  It is important to note that the arterial wall and plaque are not homogeneous; they are composed of different types of materials [5].  To accurately model these features, a different set of constitutive equations may have to be used for the different components.  Furthermore, most stents are usually made of stainless steel; some have been designed using nitinol.  To describe the nonlinear elastic behavior of stainless steel, a neo-Hookean model can be used, in which the strain energy function is

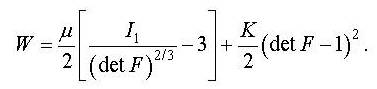
Here, I₁ is the first invariant of the B_ij, F is the deformation gradient tensor, and μ and K are the material constants.  For small deformations, μ and K refer to the shear modulus and the bulk modulus, respectively [7].  These values are related to the Young’s modulus E and the Poisson’s ratio ν.  As a result, it is possible to specify any of the two constants μ, K, E, and ν.  Most papers, such as [1] and [8], specify the Young’s modulus and the Poisson’s ratio (in addition to the yield stress σ_y).  In addition, the inelastic constitutive response of stainless steel is often described by the von Mises-Hill plasticity model with linear hardening [1].