Contents

    1. Introduction
    2. Biolocical Diffusion
    3. Diffusion Weighted Image Acquisition
    4. Diffusion Tensor Image Measures
    5. White Matter Tractography
    6. References


1. Introduction

The broad spectrum of magnetic resonance (MR) contrast mechanisms makes MRI one of the most powerful and flexible imaging modalities for the diagnosis in the central nervous system (CNS). Especially contrast mechanisms addressing functionality (i.e., fMRI, DTI), are critical for pre- and intraoperative decisions that promote the safety of the procedure and assure a successful conclusion. Measurement of signal attenuation form water diffusion is one of the most important of these contrast mechanisms. Diffusion tensor imaging (DTI) may be used to map and characterize the three- dimensional diffusion of water as a function spatial location [1]. 

The diffusion tensor describes the magnitude, the degree of anisotropy and the orientation of diffusion anisotropy. Estimates of white matter connectivity patterns in the brain may be obtained from the diffusion anisotropy and the principal diffusion directions [2]. White matter connectivity patterns, in turn, can be further explored to identify the location and the direction of white matter fiber tracks, that are important for brain integrity and may need to be preserved during neurosurgery.

Furthermore, many pathologic processes of the CNS influence the microstructual composition and architecture of effected tissues and lead to  changes in diffusion properties. Since DTI is sensitive to chances at the cellular and microstructual level, methods of acquisition and analysis of DTI are evolving rapidly. In fact, the high dimensionality of the diffusion tensor presents both challenges and novel opportunities for describing, visualizing and analyzing diffusion measurements.

2. Biological Diffusion

Diffusion is a random transport phenomenon, caused by Brownian motion, and describes the transfer of material (i.e., water) form on e spatial location to another dependent on time. The Einstein diffusion equation [3] 

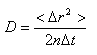             ,                                                        (Eq. 1)

 

states that the diffusion coefficient D (mm²/s) is proportional to the mean squared displacement <Δ r²> divided by the number of dimensions, n, and the diffusion time, Δt. At 20 °C the diffusion coefficient of pure water is 2.0 x 10^-3 mm²/s and increases at higher temperature. 

The molecular water displacement can be described as a Gaussian probability distribution:

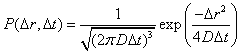.                               (Eq. 2)                                     

The diffusion of water in biological tissues occurs inside, outside, around, and through cellular structures. It is further modulated by cellular membranes and subcellular structures. Importantly, in fibrous tissue, including white matter, water diffusion is relatively unimpeded in the direction parallel to the fiber orientation, but highly restricted in the direction perpendicular to the fibers [1]. This key feature is the basis for identifying fibrous connections and pathways in white matter using DT measurements. In fact, early diffusion experiments used parallel and perpendicular diffusion components to characterize diffusion anisotropy.

It was Basser at. al. [1], who introduced the application of a diffusion tensor to describe anisotropic diffusion behaviour. In this model, diffusion is described by a multivariate normal distribution:

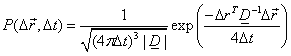         ,                     (Eq. 3)

where the diffusion tensor is a 3 by 3 covariance matrix

                        ,

   

         

which describes the covariance of diffusion displacements in three dimensions normalized by the diffusion time. The diagonal elements are the diffusion variances along the axes x, y, and z and the off diagonal elements are the covariance terms symmetric about the diagonal. Diagonalization of the diffusion tensor yields the eigenvalues (λ_1, λ_2, λ₃) and the corresponding eigenvalues (ε_1, ε_2, ε₃), which describe the directions and apparent diffusivities along the principal axes.

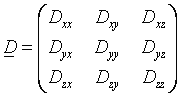The diffusion can be visualized as an ellipsoid (see Fig. 1), with the eigenvectors defining the direction of the principal axes and the eigenvalues defining the ellipsoidal radii. Diffusion is considered isotropic, if the eingenvalues are almost equal, and anistropic, if the eigenvalues are significantly different in magnitude.

        

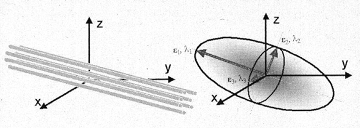
Fig. 1. Schematic representation of diffusion displacement distributions for the diffusion tensor. Ellipsoids represent diffusion displacements. The diffusion is highly anisotropic in fibrous tissues such as white matter, and the direction of greatest diffusivity is generally assumed to be parallel to the local direction of white matter.

The eigenvalue magnitude may be affected by changes in local tissue microstructure including various types of injury, disease or normal physiological changes (i.e., aging). Since, water diffusion is generally anisotropic in white matter and isotropic in both gray matter and cerebrospinal fluid (CSF), the major diffusion eigenvector (ε₁) is assumed to be parallel to the tract orientation in regions of homogeneous white matter. This directional relationship serves as a basis for estimating the trajectories of white matter pathways.

3. Diffusion Weighted Image Acquisition

The simplest and most common approach to acquire diffusion weighted images using MRI is the pulsed-gradient spin echo pulse sequence with a single-shot, echo planar imaging readout, depicted in Fig. 2.

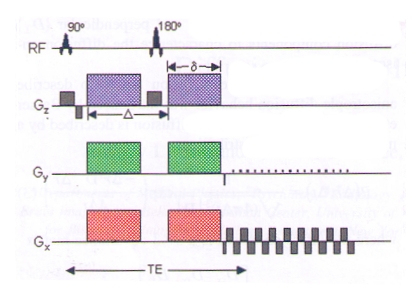
Fig. 2. Schematic of a diffusion weighted echo-planar imaging (EPI) pulse sequence. A spin echo is used to achieve a diffusion weighted image from the gradient pulse pairs  (colored gradients on each side of the 180° radiofrequency (RF) pulse). The normal EPI gradients are shown in grey.

The first gradient pulse (see Fig. 2, colored pulse on the left side of the 180° RF pulse) dephases the magnetization. the second pulse (see Fig. 2, colored pulse on the rightt of the 180° RF pulse)  rephases the magnetization, and a spin echo is sampled afterwards. For non diffusing molecules, the phases induced by both gradient pulses will cancel out and there will be no signal attenuation. In contrast, if there is diffusion in the direction of the applied gradient, there will be a net phase difference, which is proportional to the displacement and dependent on the diffusion gradient pulse pairs of amplitude G, duration δ, and spacing Δ.

Due to the displacement of diffusing water, modelled by Eq. 2, water molecules at each voxel will accumulate different phases, and there will be signal attenuation. For the described  pulse sequence (see Fig. 2) and isotropic Gaussian diffusion, the signal S can be described by:

 

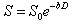,                                                                (Eq. 4)

 

where S is the diffusion weighted signal, S₀ is the signal without any diffusion weighted gradients, D is the diffusion coefficient, and b is the diffusion-weighting described by the properties of the pulse pair:

 

.                                                (Eq. 5)

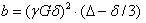
γ is the gyromagnetic ratio.

Even though EPI single shot is the most common acquisition method for DWI, there are some major problems including magnetic field inhomogeneities [4], motion artefacts [5] and eddy currents [6]. These problems are often addressed by corrections in phase direction, diffusion–weighting schemes, and image registration.
 

To measure the full diffusion tensor a minimum of six noncollinear diffusion encoding directions are required [7]. Using two- dimensional EPI pulse sequences at 1.5 T, a spatial resolution of 2.5 mm over the entire brain can be achieved in 15 minutes [8].

4. Diffusion Tensor Image Measures

The interpretation, measurement and display of a 3 by 3 diffusion matrix at each voxel is an almost  impossible task without simplification of the data. Most commonly, the trace of a tensor (Tr), the apparent diffusion coefficient MD, or the fractional anisotropy FA is used. Tr is simply the sum of the eigenvalues of D, MD is the average of eigenvalues of D, and

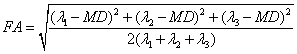,                     (Eq. 6)

 

which was fist described by Basser and Pierpaoli [9]. However, these measures may not be applicable for every quantity of interest, described by the diffusion tensor, and may need be adapted accordingly.  

A very common method in DTI is to display tensor orientation, described by the major eigenvector direction, as RGB color maps. For diffusion tensors with high anisotropy, the major eigenvector direction is generally assumed to be parallel to the direction of white matter tract, and the RGB color map is used to indicate the major eigenvector orientation. 

Quantitative maps of MD, FA, and eigenvector measures are shown in Fig. 3 bellow:

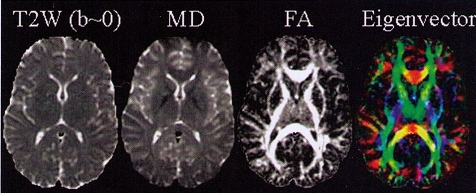
Fig 3. Quantitative maps of DTI measurements. Left to right: T2-weighted (T2W) reference image (i.e., b=0), the mean diffusivity (MD; CSF appearing hyperintense), fractional anisotropy (FA; hyperintense in white matter), the major eigenvector direction indicated by RGB color map ( red: right-left; green: anterior-posterior; blue: superior inferior) [10].

5. White Matter Tractography

Instead of simply using RGB color maps to visualize the orientation of the major eigenvector (also see Fig. 3), white matter tractography can be employed to display white matter connection in 3D. White matter tractography algorithms follow coherent spatial patterns in the major eigenvectors of the diffusion tensor field. Starting form a specified location, the direction of propagation is estimated in small subsequent steps until the tract is terminated. 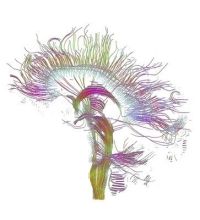Based on this method white matter trajectories can be plausibly estimated and major projection pathways estimated  (see Fig. 4).

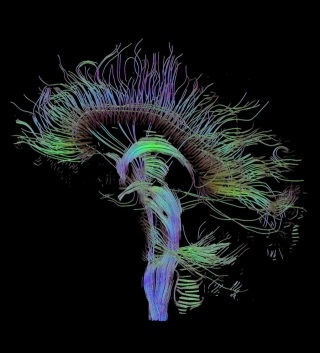
Fig. 4.  Reconstructed major fiber tracts in the mid sagi- tal  plane using  white matter tractography.