Modeling TMS

It is difficult to direct the path of the current because the brain is a non-uniform conductor with an irregular shape. Thus, in order to simulate a realistic clinical situation as accurately as possible, it is necessary to model magnetic stimulation that accounts for the complex geometry of the head and the nonhomogeneity of biological tissue.

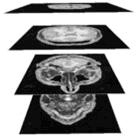
The electromagnetic problem that results is to evaluate the current distribution induced in the cortex by a magnetic pulse generator via a coil. The human head must be discretized into cubic cells as shown below in Figure 5.

Figure 5 1

To solve the problem, Maxwell’s equations must be applied to the discretized head. This discretized head can be reconstructed from MRI images, and interpolated from data in the images. Next, a knowledge of the electrical characteristics of the medium can be used to solve the electromagnetic problem by associating conductivity values of the brain tissue to the grey levels of the images. Thus, a complete 3-D model of the current distribution in the brain allows the stimulator efficiency to be estimated, its ability to focus the magnetic field in a particular area to be evaluated, and allows a check of compliance to safety standards for the patient.

In order to evaluate the electric field and current density distribution induced by an external time-varying magnetic field and generated by a current – in the head which is a non-homogeneous medium – the Maxwell’s equations in integral form must be solved.

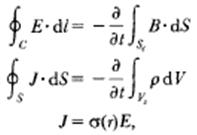
where,
E = total electric field
B = total induction field
J = conduction current density
ρ = volume charge density
σ(r) = tissue conductivity
r = the spatial coordinate
dl = an elementary length of the closed integration path C
Sc = the surface of contour C
S = the closed surface, and
Vs = the volume of surface S.

Next, we consider time and frequency characteristics of the source. The switching element that permits the capacitor to charge and discharge is generally realized with solid-state technology. This technology is subjected to very strong current pulses, creating overheating and premature aging of the elements. The fundamental parameters that determine the efficiency of magnetic stimulation are the maximum value of magnetic induction field and the repetition rate of the discharges. These depend on the power supply characteristics. In the particular application of the stimulation of the cerebral cortex, the current pulse has a repetition period of about five to ten seconds with a rise time of the order of 100 microseconds and an amplitude of thousands of amperes. A typical pulse P(t), normalized to its maximum value is shown in Figure 6.

Figure 6 – Time dependence of source current pulse normalized to its maximum value

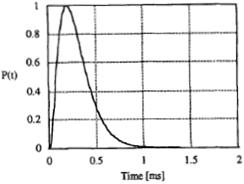
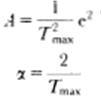This curve is well fitted by the equation , where and Tmax = 200μs.

This allows for the evaluation of the pulse spectrum, , in the closed form with its normalized amplitude shown in Figure 7.

Figure 7

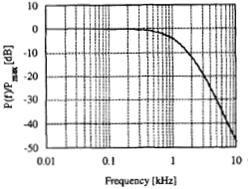
As a result of the phenomena being slow varying (in the time domain) or upper bounded to a very low frequency (in the frequency domain), we are allowed to simplify the problem. We make the following approximations:

First, the total magnetic field inside the head is given by the external field Bo due to the coil current Jo* and by the scattered field Bs due to the induced currents J given by following equation:

It can be shown that for common values of tissue conductivity the scattered field is much smaller than the external one, so the contribution of Bs to the total field can be neglected and therefore the equation becomes

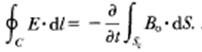
Assuming for the current in the coil, the field Bo is evaluated by 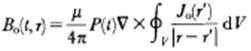, where V is the volume where the current is defined.
Second, the second of Maxwell’s equations can be written in the frequency domain as , where εr(r) is the relative permittivity of the tissue. For a typical tissue the minimum value of conductivity (about 10^-2 S/m) and the maximum value of relative permittivity (about 50), yields that tissue conductivity is significantly greater than permittivity. In the frequency stimulation range 0-10kHz, this means that

Surface charge density ρ, at any interface between tissues can be evaluated from conductivity (σ1, σ2) and permittivity (ε1, ε2).

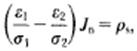
Now, we are able to solve Maxwell’s equations. The investigated region is discretized into cubic cells whose dimension is ∆. Since the minimum wavelength of the induction field is much greater than ∆, all electromagnetic quantities can be considered constant in a cell. Associating an electric field component to each edge of the cell, Kirchoff’s current law can be discretized into

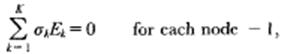, where 3 ≤ K ≤ 6 according to the position of the node (peripheral or central) and σk is the average of the conductivity values σ pertaining to the four cells surrounding the edge. The mesh equation applied to each face of the cubic cell yields:

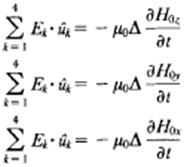
where uk is the unit vector associated with the path of the line integral and the derivative of the magnetic field is evaluated in the centre of the face.  This gives the linear system:

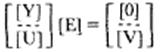
where the admittance matrix [Y] is a large sparse matrix whose non-zero elements account for the electric characteristics of the tissues, matrix [U] is a sparse matrix containing the value 1 or -1 only, and vector [V] accounts for the electromotive force induced in each mesh by the external field.

1 Starzynski, J., B. Sawicki, S. Wincenciak, A. Krawczyk, and T. Zyss. “Simulation of Magnetic Stimulation of the Brain.” IEEE Transactions On Magnetics, Vol. 38, No. 2, March 2002.

Cerri, G., De Leo, R., Moglie, F. and Schiavoni, A. (1995) 'An accurate 3-D model for magnetic stimulation of the brain cortex', Journal of Medical Engineering & Technology, 19:1, 7 — 16