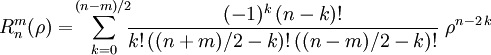A wavefront is a surface of points having the same phase. The optics of the cornea and lens change the shape of the wavefronts measured from the eye. A wavefront system reflects light off the retina through the lens and cornea, and then subtracts a planar surface from the measured wavefront that is reflect back into the instrument. After the subtracted surface is calculated, the wavefront surface is fit using Zernike polynomials or Fourier analysis. These wavefront maps show objectively the refractive error and aberrations of the optical system of the eye.
Zernike Polynomials - are a sequence of orthogonal polynomials on a unit disk.
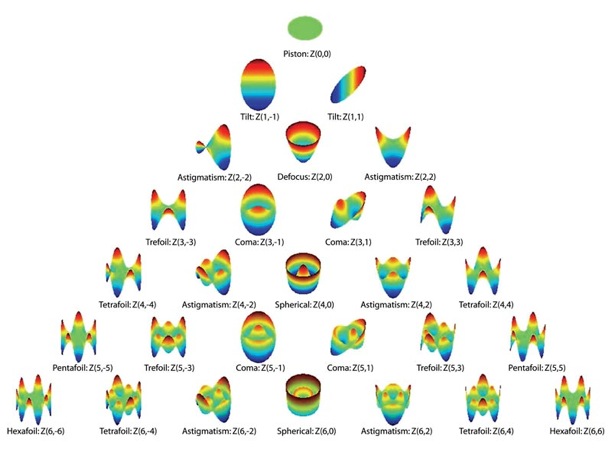
The figure above depicts the Zernike polynomials up to the 6th order. The top rows’ value contribute to lower order aberrations, where as the base of the triangle represents the high order aberrations.
Even Zernikes are defined as
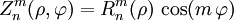
and odd as
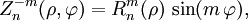
where m and n are nonnegative integers. ρ is the normalized radial distance and φ is the azimuthal angle in radians.